SEAM Calculations
SEAM = Simple, but Exact AltiMeter
This sketch shows the launching site:

m = height of eyeline above launcher L = launcher I = impact
The basic formula is tan a = h/c. Assuming the rocket goes straight up and down we can write
(1): h = r * tan a
Usually the rockets land at some distance to the launcher due to side winds or non-vertical launches. This may affect the measured altitude, if we just use (1). If we assume that the rocket lands behind the launcher as shown in the sketch above, we get
(2): tan a = h/(r+s/2)
We may watch the launch from an elevated standpoint, m meters above launch level. For the total altitude Alt of the rocket above ground level we get in this case
(3): Alt = m + h = m + (tan a) * ( r + s/2 )
However, the rocket may land not just behind the launcher, but anywhere:
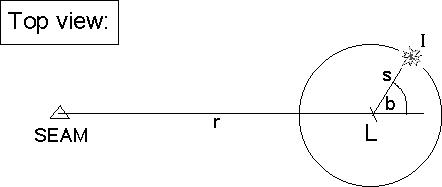
So, after impact, we measure not only the angle a and the distance to the launcher s, but as well the angle b.
Depending on the angle b, the real altitude will be greater or smaller than the basic formula (1) with c = r. This is reflected in
(4): Alt = m + tan a * (r + s/2 * cos b)
Equation (4) is a good approximation if no chute is used, meaning if the times for going up and down are similar. With a chute, the down time is much longer than the up time. To take this into account, we can write, assuming a constant side drift
(5): Alt = m + tan a * (r + s * tup/(tup + tdown) * cos b)
Usually you can neglect m. But if you are watching from some elevated standpoint, m can be determined quite nicely as follows:

We approximate r by the measured distance between SEAM and the launcher L; we measure the angle g. For m we get
(6): m = r * tan g
Now let's do a real world
EXAMPLE:
Before launch we determine m = 3,34 m and r = 40 m. Angle a is in all cases 65°. We assume tup is similar to tdown .
Case 1: no matter where the rocket landed, we use formula (1) and Alt = h + m
Case 2: the rocket landed 15,3m behind the launcher, at b=5°. Formula (4).
Case 3: the rocket landed 15,3m between the launcher and the SEAM, at b=185° . Formula (4).

As one can see, the results are quite different, depending on where the rocket landed.
Hint: If you are new to trigonometric calculations, try first if tan(45°)=1 . If it is not, your calculator or data sheet probably uses radians instead of degrees. In this case try, if tan(45*Pi/180)=1. If so, use that enhancement [angle in degrees]*Pi/180 each time when an angle has to be entered.
This page entirely created on a Psion5 palmtop on 17. Sept. 2000
![]()













